Overview
We seek to better understand brain function and dysfunction. A principal difficulty in this endeavor is that the research entails everything from behavior of molecules, on up to behavior of people. Not only must this information be gathered, it must also be linked together to provide explanation and prediction. Computational neuroscience is developing a set of concepts and techniques to provide these links for findings and ideas arising from disparate types of investigation.
Marr's Theory of Brain Theory
In his book Vision, David Marr hypothesized that the brain could best be understood using a top-down perspective:
-
Identify the problem -- what does the brain have to do?
-
Discover an algorithm -- what is the best way to solve this problem?
-
Implement in software, hardware, neural tissue or another computational medium.
By way of contrast, much of the field of neuroscience has implicitly hypothesized that that brain will be understood bottom-up: identify all of the molecules, neural types, circuits, activity patterns, etc. and somehow pull it all together just before the neuroscience meeting convenes. Both approaches are incomplete.
 One problem with Marr's problem level is that we cannot guess a priori what the Problems are that the brain, or a particular brain circuit, is designed for. A good example of this comes from vision, the topic of Marr's book. Subsequent discoveries have shown that the brain solves at least two problems: "what is it?"; "where is it?" and surely many more problems and subproblems as well.
One problem with Marr's problem level is that we cannot guess a priori what the Problems are that the brain, or a particular brain circuit, is designed for. A good example of this comes from vision, the topic of Marr's book. Subsequent discoveries have shown that the brain solves at least two problems: "what is it?"; "where is it?" and surely many more problems and subproblems as well.
We cannot find the single central problem that the brain solves, because it solves many problems. An engineer would not a priori imagine that the brain "solves" vision by breaking up the system into 2 or more streams of processing (perhaps as part of designing a workable system, he or she might hack such a system). Finally, the algorithm that the brain does use, while it surely solves problems, also creates problems. Once you have split up visual information, you need under some circumstances, likely under most non-emergency circumstances, to put the information back together. This is one part of what is referred to as the binding problem.
Further problems with the problematic Marrian Problem-based approach come when we consider the implementation level. Neurons are not transistors and they are not neural networks. It remains unclear what kind of device they are and what kind of information processing that they are able to do. They have a variety of anatomic and dynamic (physiological) features that remain unexplained: What are dendritic spines for?; What are dendrites for? What are spikes for?; What are brain waves (oscillations) for? …

All of this has led us to adapt Marr's insights by attempting to work the middle path of middle-out, with Algorithm in mid-position. Implementation largely determines what algorithms a system is capable of. It is not simply for want of clever algorithms that CMOS (the current technology of computers) cannot achieve adequate control of a bipedal robot or a flying fly. (CMOS can simulate walking and flight, but cannot do it within the constraints of space, weight, and time required. If it takes 10 minutes to calculate how much to bend the knee, the robot will fall down long before the knee begins to move.)
We can compare this difference in approach to the changes that have taken place in the philosophy, politics and practice of science. The classic top-down approach would start again with a problem, then hypothesis (cf. Popper), then the gathering of data to attempt to falsify the hypothesis. More recently, there has been growing appreciation of the usefulness of data gathering, such as the human genome project, as a complementary approach. One can't generate hypotheses in the absence of data.
Theories, models, simulation, Occam & Einstein
Einstein may have said something about theories ideally being as simple as possible but not simpler. (Closest clear quote: "goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience." This doesn't make much sense literally since of course one will have to drop a datum here and there; hence the standard paraphrase -- as simple but not simpler -- works somewhat better.) Occam also said something about explaining stuff by making as few assumptions as possible. This has been riffed on by numerous philosophers and scientists. The various paraphrases note two parts: use fewer things; use known things in preference to hypothesized things.
Our  lab simulates models that instantiate theories to provide mechanistic explanations. At each of these steps there are decisions to be made about how simple to make things. Not only is the process complex but the things (dendrites, neurons, columns, networks, areas, brains) being simulated are themselves complex. Classical physics, quantum mechanics, statistical mechanics and computer logic all study complex systems, but they study complex systems made up of simple, usually all identical, components. By contrast, the neuron is not simple like a water molecule and the brain is not like a bowl of jello. The brain is a complicated, multifaceted device made up of complex multifaceted devices, arranged in diverse (complicated) ways. Different brain areas have circuitry featuring little-understood connections such as dendrodendritic, axoaxonic, and triadic. Admittedly, it was not engineered (we're not creationists for god's sake!), but the parts and bits have evolved to fit together extremely well to produce human brains and human bodies that are well-integrated machines. For a comparison, we would want to consider a complex, well-integrated machine; like this example on the left.
lab simulates models that instantiate theories to provide mechanistic explanations. At each of these steps there are decisions to be made about how simple to make things. Not only is the process complex but the things (dendrites, neurons, columns, networks, areas, brains) being simulated are themselves complex. Classical physics, quantum mechanics, statistical mechanics and computer logic all study complex systems, but they study complex systems made up of simple, usually all identical, components. By contrast, the neuron is not simple like a water molecule and the brain is not like a bowl of jello. The brain is a complicated, multifaceted device made up of complex multifaceted devices, arranged in diverse (complicated) ways. Different brain areas have circuitry featuring little-understood connections such as dendrodendritic, axoaxonic, and triadic. Admittedly, it was not engineered (we're not creationists for god's sake!), but the parts and bits have evolved to fit together extremely well to produce human brains and human bodies that are well-integrated machines. For a comparison, we would want to consider a complex, well-integrated machine; like this example on the left.
We will not be able to develop a simple, parsimonious theory for how a Boeing 747 works. We need different models for understanding engines and thrust, hydraulics, navigation, pressurization and HVAC, emergency evacuation procedures etc. In many of these cases we will want to use multiple models at different levels of detail for particular systems. A complex model for the details of fuel combustion will be used in a reduced form in a model that considers engine thrust. A simple parsimonious theory of how wings work (Bernoulli's) will be the basis of simulations to understand the lift generated by wings in different configurations (flags, ailerons) and in different atmospheric conditions. A simulation for a single real-world flight of a machine of this complexity will require a lot of judgment as to what to include and what to omit for a particular purpose. Hence, there will necessarily be simplification, but not aggressive initial simplification that leaves out the trees in hope of understanding the forest.
Multiscale modeling - molecular, cellular, network, system
 Understanding brain dynamics and information flow is fundamentally a multiscale problem: the network scale emerges from cell dynamics, which emerge from interactions of cellular somatic and dendritic dynamics. Dynamical interactions are bidirectional at each level, and sometimes reach across multiple levels. Multiscale modeling enables us to connect these different scales: from molecular interactions, such as dendritic integration (subcellular scale; <10μm), through the cellular scale (~30μm), to the large-scale network dynamics (~1mm to ~5cm) that generate behaviors. Temporally, we must model at scales of milliseconds, for interactions between postsynaptic potentials, up to the order of >10 sec for signaling via cortical oscillations. Overall, these complex structure-function relationships cover 4 orders of magnitude both spatially and temporally, each scale providing a unique level of detail that can inform our understanding of the brain.
Understanding brain dynamics and information flow is fundamentally a multiscale problem: the network scale emerges from cell dynamics, which emerge from interactions of cellular somatic and dendritic dynamics. Dynamical interactions are bidirectional at each level, and sometimes reach across multiple levels. Multiscale modeling enables us to connect these different scales: from molecular interactions, such as dendritic integration (subcellular scale; <10μm), through the cellular scale (~30μm), to the large-scale network dynamics (~1mm to ~5cm) that generate behaviors. Temporally, we must model at scales of milliseconds, for interactions between postsynaptic potentials, up to the order of >10 sec for signaling via cortical oscillations. Overall, these complex structure-function relationships cover 4 orders of magnitude both spatially and temporally, each scale providing a unique level of detail that can inform our understanding of the brain.
The multiscale modeling approach consists of modeling small subcomponent at a given scale with a high degree of fidelity, in order to find emergent properties that can then be used as input to the next-larger scale model. Depending on modeling aims and compute resources, many elements at a scale can be replaced with a higher level lumped element that reproduces similar properties. A second complementary strategy is to use the properties of the high-level coarser model, such as network dynamics, input/output transformations or expected behaviors, as a target to fine-tune the parameters of the more biological detailed model. Finally, models of different complexity and granularity can be integrated into hybrid models, by implementing any required transformations of inputs/outputs, e.g. firing rate to Poisson-generated spikes to action potentials. In the past we have implemented all of these strategies, and will continue to develop and make use of them for this project.
Understanding neural coding through multiscale simulation
The function and organization of the brain primary motor cortex (M1) circuits -- crucial for motor control -- has not yet been resolved. Most brain-machine interfaces used by spinal cord injury patients decode their motor information from M1, predominantly from large layer 5 corticospinal cells. We have developed the most realistic and detailed computational model of M1 circuits and corticospinal neurons up to date, based on novel experimental data. The model is being used to decipher the neural code underlying the brain circuits responsible for producing movement and contribute to the advancement of brain-machine interfaces for spinal cord injury patients.
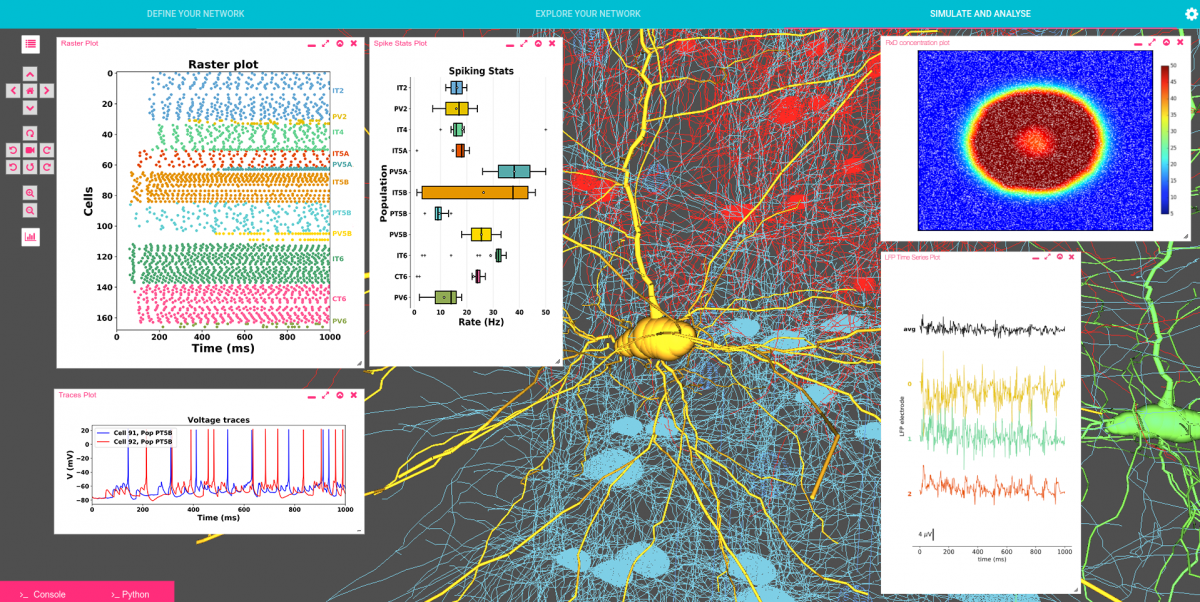
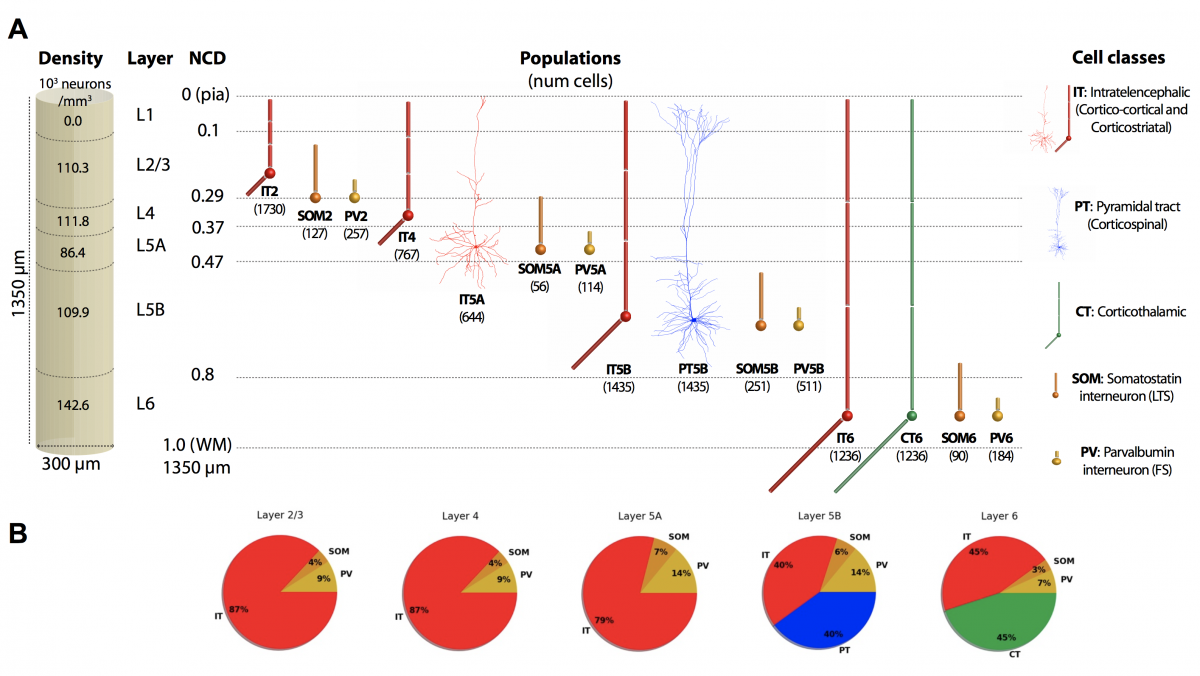 Our detailed M1 model includes over 10,000 neurons distributed across the cortical layers. Corticospinal cell models accurately reproduce the electrophysiology and morphology of real neurons. More than 30 million synaptic connections reproduce cell type- and location connectivity patterns obtained from experimental studies. It also simulates inputs from the main cortical and thalamic brain regions that project to M1. Results provide a more in-depth understanding of how long-range inputs from surrounding regions and molecular/pharmacological effects modulates M1 corticospinal output. We identified two different pathways that activated corticospinal output. Simulated local field potential (LFP) recordings revealed physiological oscillations and information flow consistent with biological data. Modulation of HCN channels in corticospinal neurons served as a switch to regulate output, a potential mechanism to convert motor planning into motor execution. Our work provides insights into how information is encoded and processed in the primary motor cortex.
Our detailed M1 model includes over 10,000 neurons distributed across the cortical layers. Corticospinal cell models accurately reproduce the electrophysiology and morphology of real neurons. More than 30 million synaptic connections reproduce cell type- and location connectivity patterns obtained from experimental studies. It also simulates inputs from the main cortical and thalamic brain regions that project to M1. Results provide a more in-depth understanding of how long-range inputs from surrounding regions and molecular/pharmacological effects modulates M1 corticospinal output. We identified two different pathways that activated corticospinal output. Simulated local field potential (LFP) recordings revealed physiological oscillations and information flow consistent with biological data. Modulation of HCN channels in corticospinal neurons served as a switch to regulate output, a potential mechanism to convert motor planning into motor execution. Our work provides insights into how information is encoded and processed in the primary motor cortex.
Our group has previously developed large-scale biomimetic models of several memory and sensory areas, including hippocampal regions (CA1 and CA3), PFC, and several neocortical regions. We focus on developing multiscale models linking the different brain spatiotemporal scales, ranging from molecular interactions through cortical microcircuit computations, to large-scale behaviors. Our models are able to accurately reproduce physiological properties observed in vivo, including firing rates, local-field potentials, oscillations and travelling waves. Our biological learning mechanisms, including LTP, LTD, STDP and RL, have been used to demonstrate the formation of short and long term memories, color opponent receptive fields, tactile receptive fields, and sensorimotor mappings, which enabled the model to control a virtual and a robotic arm.
We have also demonstrated the flexibility of our models by interfacing them with more abstract models, such as state-space models and neural field models, with BMI decoders (ongoing REPAIR work with Sanchez lab) and neural controllers (ongoing REPAIR work with Principe lab); with virtual and robotic devices; and with Plexon real-time neural acquisiton systems (ongoing REPAIR work with Fortes lab).
Dendritic processing and network synchron
The dendrites are the major functional units through which a neuron receives synaptic inputs. The properties of dendritic processing play a crucial role in synaptic integration and neural plasticity, and contribute to the action potential generation essential for neural coding. We are developing single neuron models to mimic the electrical signals in cortical pyramidal neurons by incorporating these complex dendritic properties. Experimental voltage waveforms, recorded by voltage sensitive dye in the dendrites and patch-clamps in the soma of individual neurons, provide proper constraints to the models. Simulations using the model can, in turn, make testable/falsifiable predictions to guide subsequent experimental designs. Additionally, we aim to use the single neuron models to construct realistic networks and investigate the biological details, such as oscillations and synchronizations, at the functional circuit level. Our final goal is to offer theoretical insights into how individual brain cells and complex neural circuits interact through multi-scale modeling.
 Multiscale modeling to study brain disease and disorders
Multiscale modeling to study brain disease and disorders
We have employed cortical models to study generation and prevention of epileptic seizures; a model of basal ganglia and thalamocortical circuits to study Parkinson's disease; and a model of hippocampus to study schizophrenia and how it relates to certain genetic and molecular properties.
Our detailed computational model of M1 microcircuits provides a useful tool for researchers in the field to evaluate novel hypothesis, motor disorders and decoding methods for brain-machine interfaces and pharmacological or neurostimulation treatments for motor disorders. A version of the model was used to simulate the effects of dystonia and study possible multiscale pharmacological treatments
Simulating neurostimulation
Several companies have been making inroads into the research of neuromodulation through electromagnetic stimulation, which includes transcranial direct current stimulation (tDCS), transcranial alternating current stimulation (tACS), and various methods of transcranial magnetic stimulation (TMS). However, our understanding of the underlying mechanism is underdeveloped. Simply put, neurons do not seem to be sufficient to fully model directional electromagnetic fields. We hope to shed light into this old but relevant phenomena from a single neuron to entire regions of the brain, particularly the hippocampus. This work can reveal insights into new forms of treatment that require no pharmaceutical intervention while furthering our understanding of the brain’s natural oscillation functioning.
During the REPAIR project we have also shown that our models can reproduce neural stimulation methods such pharmacological therapy (ZIP), electrical microstimulation, and optogenetic stimulation.
Biomimetic neuroprosthetics/Brain-machine interfaces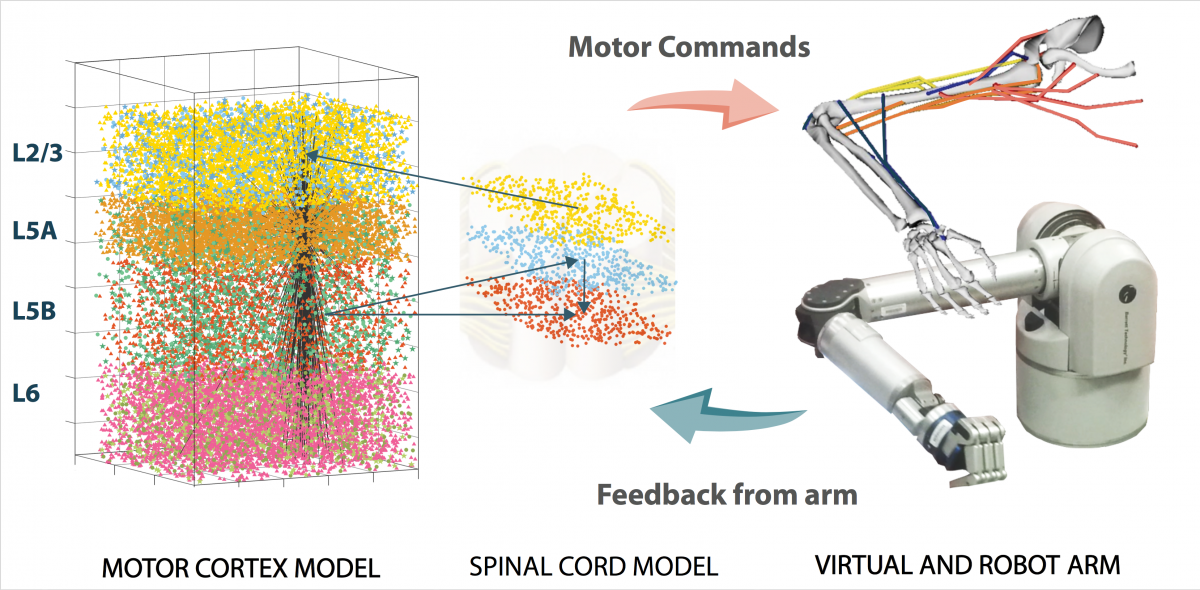
Developments in neuroprosthetics and BMIs now enable paralyzed subjects to control a humanoid robotic arm with signals recorded from multielectrode arrays implanted in their motor cortex. Latest advance also allow the user to feel the touch and proprioception by converting the robotic arm feedback signals into electrical signal that stimulate the somatosensory cortex. Combining neuroprosthetics with realistic cortical spiking models that interact directly with biological neurons and exploits biological plasticity/adaption may enable finer motor control and more naturalistic sensations. We developed a real-time interface between a NEURON-based spiking cortical model, a virtual musculoskeletal arm and a robotic arm. The model used spike-timing- dependent plasticity (STDP) and reinforcement learning (RL) to learn to control the virtual and robotic arms. We also extended the system to include real-time input of neurophysiological data recorded from non- human primates into the NEURON spiking models. The full system constituted the prototype of a biomimetic neuroprostheses that could be used as a BMI or to replace damaged brain regions with in silico counterparts.
Software for multiscale modeling
 NEURON is the leading simulator in the neural multiscale modeling domain, with thousands of users, an active forum (neuron.yale.edu/forum; >10,000 posts), over 600 immediately runnable simulations available via ModelDB, and over 1800 NEURON-based publications.
NEURON is the leading simulator in the neural multiscale modeling domain, with thousands of users, an active forum (neuron.yale.edu/forum; >10,000 posts), over 600 immediately runnable simulations available via ModelDB, and over 1800 NEURON-based publications.
We have developed tools that extend NEURON's capabilities at the molecular -- Reaction Diffusion (RxD) tool -- and the network/circuit scale -- NetPyNE (www.netpyne.org). See our Software page for more details.